Big Oh No
09 May 2016What the hell does O(log n) mean?
This can be understood by investigating the space complexity of how many bits that is needed to store an integer. (Spoiler: it's O(log n)).
Warning: nasty oneliners ahead, the output is the interesting part.
binary representation and number of bits
pry(main)> (1..16).each{|n| puts "n: %2i binary: %5s num_bits: %i" % [n, n.to_s(2), n.to_s(2).length]}
n: 1 binary: 1 num_bits: 1
n: 2 binary: 10 num_bits: 2
n: 3 binary: 11 num_bits: 2
n: 4 binary: 100 num_bits: 3
n: 5 binary: 101 num_bits: 3
n: 6 binary: 110 num_bits: 3
n: 7 binary: 111 num_bits: 3
n: 8 binary: 1000 num_bits: 4
n: 9 binary: 1001 num_bits: 4
n: 10 binary: 1010 num_bits: 4
n: 11 binary: 1011 num_bits: 4
n: 12 binary: 1100 num_bits: 4
n: 13 binary: 1101 num_bits: 4
n: 14 binary: 1110 num_bits: 4
n: 15 binary: 1111 num_bits: 4
n: 16 binary: 10000 num_bits: 5
It seems like the number of bits increases more slowly over time. To get more insight I counted how long the number of bits stays the same until it needs to increase (2 bits is used 2 times, 3 bits is used 4 times etc. as seen above)
numbers until adding a new bit
pry(main)> (1..1023).map{|n| n.to_s(2).length}.chunk{|n| n}.map{|n| n.last.length}
=> [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]
These numbers are looking quite familiar. At this point we are obviously working with powers of 2, and my gut is telling me that the complexity is probably \(O(\sqrt{n})\), the graph seems to even out in a similar way, right?
plotting the square root
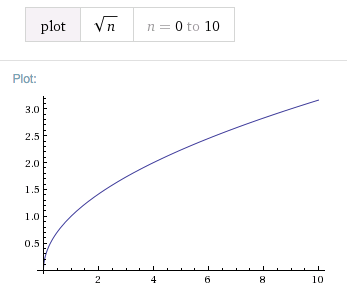
pry(main)> (1..16).each{|n| puts "n: %4i binary: %12s num_bits: %2i sqrt(n): %i" % [n, n.to_s(2), n.to_s(2).length, Math.sqrt(n).ceil]}
n: 1 binary: 1 num_bits: 1 sqrt(n): 1
n: 2 binary: 10 num_bits: 2 sqrt(n): 2
n: 3 binary: 11 num_bits: 2 sqrt(n): 2
n: 4 binary: 100 num_bits: 3 sqrt(n): 2
n: 5 binary: 101 num_bits: 3 sqrt(n): 3
n: 6 binary: 110 num_bits: 3 sqrt(n): 3
n: 7 binary: 111 num_bits: 3 sqrt(n): 3
n: 8 binary: 1000 num_bits: 4 sqrt(n): 3
n: 9 binary: 1001 num_bits: 4 sqrt(n): 3
n: 10 binary: 1010 num_bits: 4 sqrt(n): 4
n: 11 binary: 1011 num_bits: 4 sqrt(n): 4
n: 12 binary: 1100 num_bits: 4 sqrt(n): 4
n: 13 binary: 1101 num_bits: 4 sqrt(n): 4
n: 14 binary: 1110 num_bits: 4 sqrt(n): 4
n: 15 binary: 1111 num_bits: 4 sqrt(n): 4
n: 16 binary: 10000 num_bits: 5 sqrt(n): 4
When adding the rounded square root to our little table, it looks quite promising. I think I'm onto something here, but if we throw some bigger numbers at it we are quickly disappointed:
square root continued
[30] pry(main)> (1..1023).step(100).each{|n| puts "n: %4i binary: %12s num_bits: %2i sqrt(n): %i" % [n, n.to_s(2), n.to_s(2).length, Math.sqrt(n).ceil]}
n: 1 binary: 1 num_bits: 1 sqrt(n): 1
n: 101 binary: 1100101 num_bits: 7 sqrt(n): 11
n: 201 binary: 11001001 num_bits: 8 sqrt(n): 15
n: 301 binary: 100101101 num_bits: 9 sqrt(n): 18
n: 401 binary: 110010001 num_bits: 9 sqrt(n): 21
n: 501 binary: 111110101 num_bits: 9 sqrt(n): 23
n: 601 binary: 1001011001 num_bits: 10 sqrt(n): 25
n: 701 binary: 1010111101 num_bits: 10 sqrt(n): 27
n: 801 binary: 1100100001 num_bits: 10 sqrt(n): 29
n: 901 binary: 1110000101 num_bits: 10 sqrt(n): 31
n: 1001 binary: 1111101001 num_bits: 10 sqrt(n): 32
adding the logarithm
Now it's time to see if logarithms are the answer to this, when adding them into our table it works out beautifully. Here it is for some bigger numbers:
pry(main)> (1..10000).step(1000).each{|n| puts "n: %4i binary: %14s num_bits: %2i log2(n): %2i sqrt(n): %i" % [n, n.to_s(2), n.to_s(2).length, Math.log2(n).ceil, Math.sqrt(n).ceil]}
n: 1 binary: 1 num_bits: 1 log2(n): 0 sqrt(n): 1
n: 1001 binary: 1111101001 num_bits: 10 log2(n): 10 sqrt(n): 32
n: 2001 binary: 11111010001 num_bits: 11 log2(n): 11 sqrt(n): 45
n: 3001 binary: 101110111001 num_bits: 12 log2(n): 12 sqrt(n): 55
n: 4001 binary: 111110100001 num_bits: 12 log2(n): 12 sqrt(n): 64
n: 5001 binary: 1001110001001 num_bits: 13 log2(n): 13 sqrt(n): 71
n: 6001 binary: 1011101110001 num_bits: 13 log2(n): 13 sqrt(n): 78
n: 7001 binary: 1101101011001 num_bits: 13 log2(n): 13 sqrt(n): 84
n: 8001 binary: 1111101000001 num_bits: 13 log2(n): 13 sqrt(n): 90
n: 9001 binary: 10001100101001 num_bits: 14 log2(n): 14 sqrt(n): 95
Success!
Note that I'm using 2 as the base for the logarithm, the normal log function
has a base of e.
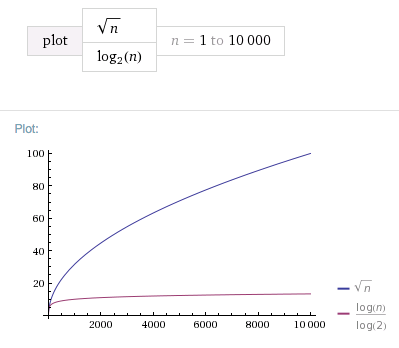
This shows how amazingly good logarithmic complexity actually is, maths is cool.
Learnings
- \(\sqrt{n}\) finds x in \(x^2=n\)
- \(log_{2}(n)\) finds x in \(2^x=n\)
- logarithmic complexity is crazy good, almost O(1).