Big Oh No

What the hell does O(log n) mean?

This can be understood by investigating the space complexity of how many bits that is needed to store an integer. (Spoiler: it's O(log n)).

Warning: nasty oneliners ahead, the output is the interesting part.

binary representation and number of bits

pry(main)> (1..16).each{|n| puts "n: %2i    binary: %5s    num_bits: %i" % [n, n.to_s(2), n.to_s(2).length]}
n:  1    binary:     1    num_bits: 1
n:  2    binary:    10    num_bits: 2
n:  3    binary:    11    num_bits: 2
n:  4    binary:   100    num_bits: 3
n:  5    binary:   101    num_bits: 3
n:  6    binary:   110    num_bits: 3
n:  7    binary:   111    num_bits: 3
n:  8    binary:  1000    num_bits: 4
n:  9    binary:  1001    num_bits: 4
n: 10    binary:  1010    num_bits: 4
n: 11    binary:  1011    num_bits: 4
n: 12    binary:  1100    num_bits: 4
n: 13    binary:  1101    num_bits: 4
n: 14    binary:  1110    num_bits: 4
n: 15    binary:  1111    num_bits: 4
n: 16    binary: 10000    num_bits: 5

It seems like the number of bits increases more slowly over time. To get more insight I counted how long the number of bits stays the same until it needs to increase (2 bits is used 2 times, 3 bits is used 4 times etc. as seen above)

numbers until adding a new bit

pry(main)> (1..1023).map{|n| n.to_s(2).length}.chunk{|n| n}.map{|n| n.last.length}
=> [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]

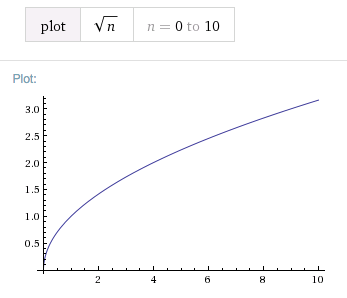
These numbers are looking quite familiar. At this point we are obviously working with powers of 2, and my gut is telling me that the complexity is probably \(O(\sqrt{n})\), the graph seems to even out in a similar way, right?

plotting the square root

pry(main)> (1..16).each{|n| puts "n: %4i    binary: %12s    num_bits: %2i    sqrt(n): %i" % [n, n.to_s(2), n.to_s(2).length, Math.sqrt(n).ceil]}
n:    1    binary:            1    num_bits:  1    sqrt(n): 1
n:    2    binary:           10    num_bits:  2    sqrt(n): 2
n:    3    binary:           11    num_bits:  2    sqrt(n): 2
n:    4    binary:          100    num_bits:  3    sqrt(n): 2
n:    5    binary:          101    num_bits:  3    sqrt(n): 3
n:    6    binary:          110    num_bits:  3    sqrt(n): 3
n:    7    binary:          111    num_bits:  3    sqrt(n): 3
n:    8    binary:         1000    num_bits:  4    sqrt(n): 3
n:    9    binary:         1001    num_bits:  4    sqrt(n): 3
n:   10    binary:         1010    num_bits:  4    sqrt(n): 4
n:   11    binary:         1011    num_bits:  4    sqrt(n): 4
n:   12    binary:         1100    num_bits:  4    sqrt(n): 4
n:   13    binary:         1101    num_bits:  4    sqrt(n): 4
n:   14    binary:         1110    num_bits:  4    sqrt(n): 4
n:   15    binary:         1111    num_bits:  4    sqrt(n): 4
n:   16    binary:        10000    num_bits:  5    sqrt(n): 4

When adding the rounded square root to our little table, it looks quite promising. I think I'm onto something here, but if we throw some bigger numbers at it we are quickly disappointed:

square root continued

[30] pry(main)> (1..1023).step(100).each{|n| puts "n: %4i    binary: %12s    num_bits: %2i    sqrt(n): %i" % [n, n.to_s(2), n.to_s(2).length, Math.sqrt(n).ceil]}
n:    1    binary:            1    num_bits:  1    sqrt(n): 1
n:  101    binary:      1100101    num_bits:  7    sqrt(n): 11
n:  201    binary:     11001001    num_bits:  8    sqrt(n): 15
n:  301    binary:    100101101    num_bits:  9    sqrt(n): 18
n:  401    binary:    110010001    num_bits:  9    sqrt(n): 21
n:  501    binary:    111110101    num_bits:  9    sqrt(n): 23
n:  601    binary:   1001011001    num_bits: 10    sqrt(n): 25
n:  701    binary:   1010111101    num_bits: 10    sqrt(n): 27
n:  801    binary:   1100100001    num_bits: 10    sqrt(n): 29
n:  901    binary:   1110000101    num_bits: 10    sqrt(n): 31
n: 1001    binary:   1111101001    num_bits: 10    sqrt(n): 32

adding the logarithm

Now it's time to see if logarithms are the answer to this, when adding them into our table it works out beautifully. Here it is for some bigger numbers:

pry(main)> (1..10000).step(1000).each{|n| puts "n: %4i    binary: %14s    num_bits: %2i    log2(n): %2i    sqrt(n): %i" % [n, n.to_s(2), n.to_s(2).length, Math.log2(n).ceil, Math.sqrt(n).ceil]}
n:    1    binary:              1    num_bits:  1    log2(n):  0    sqrt(n): 1
n: 1001    binary:     1111101001    num_bits: 10    log2(n): 10    sqrt(n): 32
n: 2001    binary:    11111010001    num_bits: 11    log2(n): 11    sqrt(n): 45
n: 3001    binary:   101110111001    num_bits: 12    log2(n): 12    sqrt(n): 55
n: 4001    binary:   111110100001    num_bits: 12    log2(n): 12    sqrt(n): 64
n: 5001    binary:  1001110001001    num_bits: 13    log2(n): 13    sqrt(n): 71
n: 6001    binary:  1011101110001    num_bits: 13    log2(n): 13    sqrt(n): 78
n: 7001    binary:  1101101011001    num_bits: 13    log2(n): 13    sqrt(n): 84
n: 8001    binary:  1111101000001    num_bits: 13    log2(n): 13    sqrt(n): 90
n: 9001    binary: 10001100101001    num_bits: 14    log2(n): 14    sqrt(n): 95

Success!

Note that I'm using 2 as the base for the logarithm, the normal log function has a base of e.

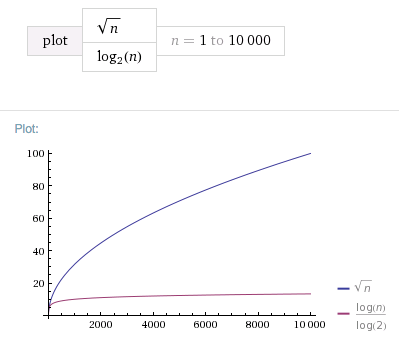
This shows how amazingly good logarithmic complexity actually is, maths is cool.

Learnings

• \(\sqrt{n}\) finds x in \(x^2=n\)
• \(log_{2}(n)\) finds x in \(2^x=n\)
• logarithmic complexity is crazy good, almost O(1).

Use word boundary regex matches

How do you search for a word?

• "word" will also match "swordsmanship"
• " word " will miss "word: "
• etc.

The answer is simple: word boundaries.

In PCRE (which is a very widely used regex engine, you are likely using this) you can do \bword\b, or in Vim's regex engine you can do \<word\> and it does exactly what you want.

Address already in use

Sometimes, you find yourself with a local web server running, but having lost the console session where you started it, so you can't ctrl-c to stop it. Maybe you closed the tab, or the terminal crashed leaving the server running. When you try to start the server again you an error like Address already in use, or A server is already running.

For a long time I didn't really have a solution for this, it didn't happen very frequently so I just started the server on a different port and moved on with my life.

Some time ago I finally did the research and came up with a better solution. It is a very simple bash script that simply kills whichever process that listens to the port you give it, I call it portkill - Here it is in action:

It gets the id of the process listening on the port using lsof -t -i:4000, then simply kills that process. Here is the source of portkill, with a tiny bit of error handling.

Emacs without Emacs

Vim is a very expressive language for editing text, and many other tools provide Vim-style key bindings to interact with them, although the Emacs-style key bindings are often the default. (They are actually from Readline, which uses Emacs-ish bindings, but some of them are different, notably <C-u> works differently than in Emacs)

Most Vim emulators provide very limited and inconsistent behaviour (except for, ironically, Emacs), but I also find that in a command prompt, the Emacs bindings are more pleasant to work with. In this context, you usually only want to perform one or two actions, so switching between modes is both tedious and confusing, especially when it does not quite behave as full Vim would do anyway.

Here are the mappings I use most frequently in bash or basically any command prompt or REPL. Try them in other programs - you might be surprised by how often they work.

• <C-a> goes to the beginning of the line
• <C-e> goes to the end of the line
• <C-f> and <C-b> goes forward and backward by character
• <M-f> and <M-b> goes forward and backward by word
• <C-u> removes everything before the cursor
• <C-k> removes everything after the cursor

You might need to tweak the settings of your terminal emulator for the alt/meta key to be sent through properly.

I find these mappings much more appropriate when using a command prompt application, and if you ever need the full power of Vim, you can start a full Vim session to edit the command with <C-x><C-e>.

vimrc best practices

Well designed software is easy to change. The more often it changes, the more important it is that it is well designed. VimScript is code, and at least in my case, it certainly changes often. Even though I don't write sophisticated plugins, the vimrc still calls for some level of style and consistency.

Here are some standards I've found to be helpful to keep things tidy:

1. Be specific with mappings

• Always use the noremap bindings unless you absolutely have to use the normal one. Using nmap instead of nnoremap has caused me many headaches.
• Use xnoremap. This is a bit of a sneaky one, vnoremap, despite its seemingly obvious name maps both visual and select mode - xnoremap maps only visual mode, which is usually what you mean.

2. Use single quoted strings

VimScript uses the " character for comments, strings and registers. Two responsibilities is plenty.

3. Use the same casing for mappings as Vim itself

Vim allows you to specify chords and special keys case insensitively, I suggest sticking to the same style Vim itself uses:

<Esc>, <C-a>, <CR>, <S-Down>

It is not always obvious, refer to :help key-notation when in doubt.

Update: I've opted to use the "correct" case for the "a" in <C-a>, even though Vim does not always do this itself. Terminals cannot always distinguish between C-a and C-A (or C-S-a), but in certain places (for example sometimes in NeoVim) this distinction is actually made.

Bonus: Lint your settings

There's a VimScript linter called vint that will point out many other potential problems - very handy if you want to be extra tidy.